女朋友都能听得懂的——反向传播算法
那是一个风和日丽的下午,坐在沙发上撸着猫的女朋友突然问道:”你天天标榜自己是「算法工程师」,那你觉得最厉害的算法是什么?给我讲讲呗~”
我顿时一愣,心里嘀咕着:”虽然厉害的算法有很多,但是最厉害的算法还真不好评估。而且这种什么条件都不说,上来就问最厉害的是啥的,一般都会被我归为杠精!”
我扭过头去,正寻思着给她讲讲著名的「没有免费午餐定理」(即在没有任何背景的情况下,所有算法的性能相同)的时候,她突然停止撸猫,瞥了我一眼:”你是不是不会啊?”
“哼,怎么可能~最厉害的算法当然是「反向传播算法」啦!”说完,我深深的吸了一口气。”下面你可要仔细听,这个算法有点难哦~”
女朋友示意让猫从她腿上跳下去,然后双手拄着脸,盯着我说:”我听着,你说吧,今天你要是给我讲不明白这个什么反向算法,晚饭就喝西北风吧!”
我又深吸了一口气,拿起桌子上的水杯,喝了一大口。
「反向传播算法」作为深度学习的基石,是每位数据科学家必备的知识。因此各大公司在面试时,也特别喜欢出「推演反向传播公式」这道题,用于考察面试者的基本能力。
今天我要用简单的浅层神经网络,尝试解决经典的「异或问题」。主要涉及的知识点有:激活函数、梯度下降、反向传播等。
1 异或问题
1.1 简介
异或是一种简单的运算,规则为「相同为 0,不同为 1」。由于它的英文名称是 exclusive OR,通常缩写成 XOR 或 xor。异或的数学符号表示为$\oplus$。
下面列举二进制异或运算的所有情况:
- $0 \oplus 0 = 0$
- $1 \oplus 0 = 1$
- $0 \oplus 1 = 1$
- $1 \oplus 1 = 0$
那么异或问题被定义为:构建一个算法,使其在输入为[[0, 0], [1, 0], [0, 1], [1, 1]],得到输出[0, 1, 1, 0]。
1.2 网络结构
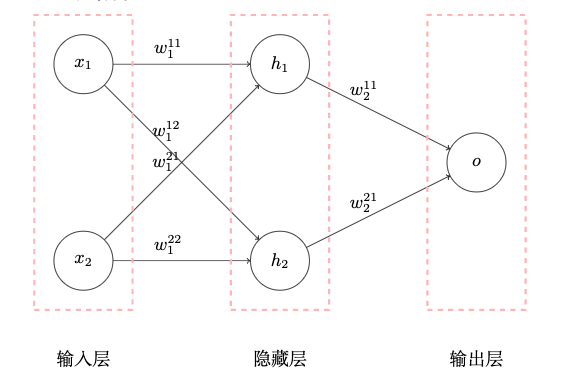
如上图所示,我们用两层的神经网络尝试解决 XOR 问题。其中隐藏层和输出层分别有 2 和 1 个神经元,后面跟着激活函数 $\sigma(·)$。
通常情况下,我们会把输入的数据叫做输入层,但其实这一层并没有神经网络,所以上述神经网络只有两层。
2 正向传播
$$
h_1 = w_1^{11} x_1 + w_1^{21} x_2 \\
\hat{h_1} = f_{sigmoid}(h_1) \\
h_2 = w_1^{12} x_1 + w_1^{22} x_2 \\
\hat{h_2} = f_{sigmoid}(h_2) \\
o = w_2^{11} \hat{h_1} + w_2^{21} \hat{h_2} \\
\hat{o} = f_{sigmoid}(o) \\
Cost = (\hat{o} - y)^2
$$
3 激活函数
3.1 简介
上文提到,我们会在每个神经元后面加一个激活函数,那么它有什么作用呢?
激活函数是为神经网络引入非线性因素。
常见的激活函数有很多,比如 Sigmoid、Softmax、ReLU、TanH 等。这里我们先介绍简单的 Sigmoid 函数。
3.2 Sigmoid 函数
Sigmoid 函数是一种 S 型函数,可以将变量映射到 (0, 1)
之间,是一种非线性的变换。
Sigmoid 函数定义为:
$$f(x)=\frac{1}{1+e^{-x}}$$
3.3 Sigmoid 求导
神经网络通常会使用梯度下降的方法训练模型,因此 Sigmoid 的求导是必不可少的一步。
$$
\begin{aligned}
f(x)’ &= (\frac{1}{1+e^{-x}})’ \\
&= -\frac{1}{(1+e^{-x})^2}(1+e^{-x})’ \\
&= -\frac{e^{-x}}{(1+e^{-x})^2}(-x)’ \\
&= \frac{e^{-x}}{(1+e^{-x})^2} \\
&= \frac{1}{1+e^{-x}}-\frac{1}{(1+e^{-x})^2} \\
&= f(x)(1-f(x))
\end{aligned}
$$
如上文公式所示,Sigmoid 函数的求导结果由自身构成,而且特别简单,所以被经常使用。
4 梯度下降
我们是如何通过训练神经网络来解决异或问题的呢?核心方法就是梯度下降法。
首先计算神经网络的输出和预期输出的均方误差,得到二者之间的差距。
假设神经网络的最后一层的输出是 $\hat{o}$,预期输出为 $y$,那么单个样本的代价函数为:
$$
Cost = (\hat{o} - y)^2
$$
代价函数有很多种,我们这里使用的叫做均方误差 MSE。
下面来看对于 n 个样本的整体代价函数:
$$
\begin{aligned}
Cost_{all} &= \frac{1}{n}\sum_{1}^n Cost + \lambda \\
&= \frac{1}{n}\sum_{1}^n (\hat{o} - y)^2 + \lambda
\end{aligned}
$$
这里的$\lambda$为权重衰减项,也称正则化项,目的是为了减小权重幅度,防止过拟合。不了解对理解本文不会有影响,在下文的公式中会直接省略。
根据代价函数的定义可知,只要最小化代价函数的值就可以得到我们期望的神经网络。
首先我们要给每一个参数随机初始化一个较小的值,为什么是随机和较小的呢?
如果是全部一样的初始值会导致什么问题呢?所有的隐藏单元都变成了与输入值有关的相同函数,失去了神经网络可以拟合任意函数的意义。
如果是一些较大的初始值会导致什么问题呢?一般情况下,神经网络会有很多层,后面的层的计算量会非常巨大,给训练带来不必要的困难。
梯度下降法中,我们每次都要对参数$w$和$b$进行更新,其中$\eta$
为学习速率,用于控制梯度更新的大小。
$$
w = w - \eta\frac{\partial Cost }{\partial w} \\
b = b - \eta\frac{\partial Cost }{\partial b}
$$
5 反向传播
上文的梯度更新中的关键步骤就是计算偏导数,通常使用反向传播来解决它。
反向传播的步骤简述如下:
正向传播。
计算最后一层的梯度;
依次从后向前计算每一层的梯度直到第一层。
下面我们来具体计算最后一层的梯度:
$$
\begin{aligned}
\frac{\partial Cost}{\partial w_2^{11}} &= \frac{\partial Cost}{\partial \hat{o}} \cdot \frac{\partial \hat{o}}{\partial o} \cdot \frac{\partial o}{\partial w_2^{11}} \\
&= \frac{\partial (y-\hat{o})^2}{\partial \hat{o}} \cdot \frac{\partial f_{sigmoid}(o)}{\partial o} \cdot \frac{\partial (w_2^{11} \hat{h_1} + w_2^{21} \hat{h_2})}{\partial o} \\
&= 2(y-\hat{o}) \cdot \hat{o}(1-\hat{o}) \cdot \hat{h_1}
\end{aligned}
$$
上面是对输出层的梯度求解,那么隐藏层的梯度呢?
$$
\begin{align}
\frac{\partial Cost}{\partial w_1^{11}} &= \frac{\partial Cost}{\partial \hat{o}} \cdot \frac{\partial \hat{o}}{\partial o} \cdot \frac{\partial o}{\partial \hat{h_1}} \cdot \frac{\partial \hat{h_1}}{\partial h_1} \cdot \frac{\partial h_1}{\partial w_1^{11}} \\
&= \frac{\partial (y-\hat{o})^2}{\partial \hat{o}} \cdot \frac{\partial f_{sigmoid}(o)}{\partial o} \cdot \frac{\partial (w_2^{11} \hat{h_1} + w_2^{21} \hat{h_2})}{\partial \hat{h_1}}\\
&\quad \cdot \frac{\partial f_{sigmoid}(h_1)}{\partial h_1} \cdot \frac{\partial (w_1^{11} x_1 + w_1^{21} x_2)}{\partial w_1^{11}} \\
&= 2(y-\hat{o}) \cdot \hat{o}(1-\hat{o}) \cdot w_2^{11} \cdot \hat{h}(1-\hat{h}) \cdot x_1
\end{align}
$$
这种依次向前求导就是所谓的「反向传播」算法。
6 代码
1 | # ! pip install torch==1.6.0 |
7 参考
女朋友都能听得懂的——反向传播算法






