排序算法简介

排序应该是最基础的算法了，在计算机的各个地方都会用到，这里我们来总结一下常见的 9 种排序算法～

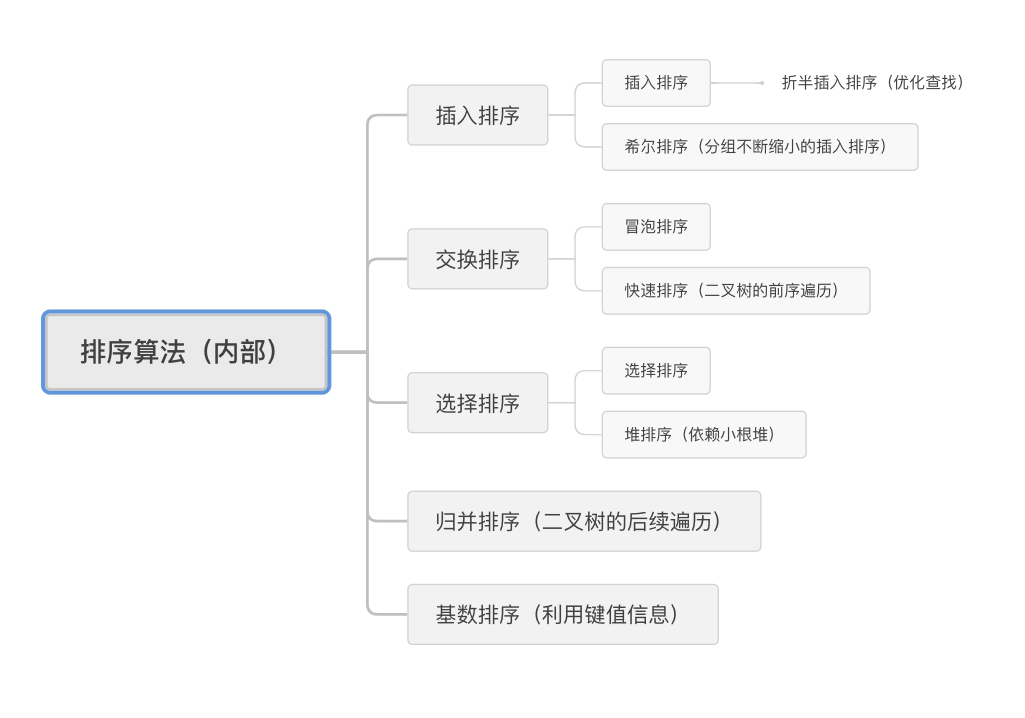
1 插入排序

简单的插入排序就是把一个无序的序列逐渐插入到一个有序的序列。

# 有序序列       无序序列
[]              [3, 2, 5, 4, 1]

[3]             [2, 5, 4, 1]
[2, 3]          [5, 4, 1]
[2, 3, 5]       [4, 1]
[2, 3, 4, 5]    [1]
[1, 2, 3, 4, 5] []

在把无序序列中的元素插入到有序序列时，需要找到合适位置。如果直接遍历的话，这个时间复杂度是 O(n)，而我们可以通过二分查找降低找到合适位置的时间，把时间复杂度变成 O(log n)。这就是折半插入排序。

当一个序列非常大，又基本有序时，我们可以通过分组插入的方式来排序。随着分组不断缩小，序列会变得越来越有序。

# 无序序列
[1, 2, 6, 5, 4, 3, 8, 7]

# 分组间距为 4 时
[1, 4] [2, 3] [6, 8], [5, 7]
# 分组间距为 2 时
[1, 6, 4, 8] [2, 5, 3, 7]
[1, 4, 6, 8] [2, 3, 5, 7]
# 分组间距为 1 时，进行简单插入排序
[1, 2, 4, 3, 6, 5, 8, 7]
[1, 2, 3, 4, 5, 6, 7, 8]

这种排序方法被称为希尔（shell）排序，以其设计者 Donald Shell 的名字命名。

虽然有一些优化方法，但插入排序每次只能将数据移动一位，在效率上是非常低的。

2 交换排序

如果一个元素的后一个位置比当前位置小，那么就交换它们，这就是冒泡排序，最大的数字原先如果在底部位置，就会像一个气泡一样逐渐升到最高，这个过程犹如海底的气泡，不断向上升至水面，因此得名。

# 无序序列
[3, 2, 5, 4, 1]
[2, 3, 5, 1, 4]
[2, 3, 1, 4, 5]
[2, 1, 3, 4, 5]
[1, 2, 3, 4, 5]

如果你只能记住一个排序算法，那么一定要记住下面这个排序算法——快速排序，就如同它的名字一样，最大的特点就是快！

快速排序的基本思想是分而治之，流程简述如下：

1. 找到一个枢纽；（可以随机找一个，也可以从头从尾部开始选）
2. 左指针和右指针从两端开始向内进行搜索，当左指针找到一个比枢纽大的，右指针找到一个比枢纽小的，就它们进行交换，直到两个指针相遇，就把枢纽放在相遇的地方。此时枢纽的位置就确定了，左侧的位置上的数字一定比枢纽小，右边的位置上的数字一定比枢纽大。（这个步骤称为一次划分）
3. 可以把枢纽左右侧分别看成一个待排序的子序列，对它们分别进行一次划分。这时又会有两个枢纽位置有序，递归的执行下去，直到所有的序列位置都有序。

# 无序序列
[5, 2, 6, 1, 4, 3, 8, 7]

# 取 5 为枢纽
[5] [2, 6, 1, 4, 3, 8, 7]
[5] [2, 3, 1, 4, 6, 8, 7]
[2, 3, 1, 4] [5] [6, 8, 7]

# 左右两边分别取 2 和 6 为枢纽
[2] [1, 3, 4] [5] [6] [8, 7]
[1] [2] [3, 4] [5] [6] [8] [7]
[1] [2] [3, 4] [5] [6] [7] [8]
[1, 2, 3, 4, 5, 6, 7, 8]

我们来用 Python 实现一下代码：

def partition(seq, left, right):
    # 选择左边第一个为枢纽
    pivot = seq[left]
    start = left + 1
    end = right
 
    while start <= end:
        # 从左向右找到一个比枢纽小的值
        while start <= end and seq[end] >= pivot:
            end -= 1

        # 从右向左找到一个比枢纽大的值
        while start <= end and seq[start] <= pivot:
            start += 1

        # 交换两个值
        if start <= end:
            seq[start], seq[end] = seq[end], seq[start]
    
    # 枢纽归位
    seq[left], seq[end] = seq[end], seq[left]
    return end

def quick_sort(seq, left, right):
    if left >= right:
        return

    pi = partition(seq, left, right)
    # 递归调用，对子序列划分
    quick_sort(seq, left, pi-1)
    quick_sort(seq, pi+1, right)

不知道你有发现快速排序有点像某种数据结构的遍历，没错！就是二叉树的先序遍历。最先的找到的枢纽相当于二叉树的根结点，而左边的序列和右边的序列就是二叉树的左子树和右子树！这样理解是不是又开启来一个新的视角呢～

3 选择排序

最简单的选择排序就是每次选择出无序序列中的最小元素，然后把它放到有序序列的最后面。

# 有序序列       无序序列
[]              [3, 2, 5, 4, 1]

[1]             [3, 2, 5, 4]
[1, 2]          [3, 5, 4]
[1, 2, 3]       [5, 4]
[1, 2, 3, 4]    [5]
[1, 2, 3, 4, 5] []

这种方法其实非常低效，实际使用过程中，我们会用一种更高效的数据结构，来完成最小值的获取，即小根堆。

小根堆是一种特殊的二叉树，它的特殊之处在于根结点永远是最小的，这样每次只需要取根结点的元素就完成来选择排序。当然每次取走小根堆的堆顶元素后，剩余的结点需要重新维护操作才能形成新的小根堆。

堆排序效率为 O(n*log n)，比一般的选择排序不少，由于小根堆的生成和维护过程比较复杂，这里就不详细介绍了，如果后续有介绍二叉树的文章再补（挖坑）。

4 归并排序

归并排序和前面的快速排序一样，也是一种分治算法。它可以看成二叉树的后续遍历，具体流程是先把所有序列分成两个一组进行排序，排好序后再把两个归并成四个进行排序，这样一直归并下去，直到所有序列都进行了排序，形成有序序列。

# 无序序列
[5, 2, 6, 1, 4, 3, 8, 7]

[5, 2] [6, 1] [4, 3] [8, 7]
[2, 5] [1, 6] [3, 4] [7, 8]
[2, 5, 1, 6] [3, 4, 7, 8]
[1, 2, 5, 6] [3, 4, 7, 8]
[1, 2, 5, 6, 3, 4, 7, 8]
[1, 2, 3, 4, 5, 6, 7, 8]

5 基数排序

基数排序简称鸡排（误～），哈哈哈！

这是我们要介绍的最后一种排序了，它也是这里面最特殊的一种排序，利用元素的键值信息进行排序。

# 比如有以下几个数据 
[18, 24, 15, 32, 22, 25]

# 先根据这几个数字的十位进行排序
[18, 15] [24, 22, 25] [32]

# 然后在根据个位进行排序
[15, 18] [22, 24, 25] [32]
[15, 18, 22, 24, 25, 32]

理解起来是不是很简单直观，由于基数排序的操作代价较小，在合适设计的情况下，甚至能快过快速排序！

以上就是常见的 9 种内部排序算法，为啥是内部呢？因为上述算法的数据都是可以在内存中放下的量，如果内存一次无法放完所有数据，就要使用外部排序算法，这种情况很少碰到，我们以后再聊（继续挖坑）。

参考

• Ailln/algorithm-python: quick sort
• 东哥手把手带你刷二叉树（第一期）